一、基本操作
有序集合也是集合的一种,顾名思义,它和集合的不同之处在于它是有序的 ,而集合无序。它通过给集合中每一个元素都关联一个分数来是的元素有序,同时提供了多个方式获取排序之后的元素。
1.1 增加和删除元素
增加元素:
|
1 |
ZADD key score member [score member ...] |
当 key 不存在时自动创建,分数支持整数和双精度浮点数,同时还可以使用+inf 和-inf 分别表示正无穷大和负无穷大。执行成功返回添加的元素个数。
删除元素:
|
1 |
ZREM key member [member ...] |
移除元素,返回成功移除的个数。
示例:
|
1 2 3 4 5 6 |
# 增加元素 127.0.0.1:6379> zadd age 24 maqian 25 xiaoming 26 xiaobai (integer) 3 # 移除元素 127.0.0.1:6379> zrem age maqian (integer) 1 |
1.2 获取元素
获取元素有以下几个操作:
|
1 2 3 4 5 6 7 8 |
# 获取有序集合中元素的数量 ZCARD key # 获取某个元素的分数 ZSCORE key member # 获取某个元素的排名 (正序) ZRANK key member # 获取某个元素的排名 (逆序) ZREVRANK key member |
注意事项:所有的排名都是从 0 开始的。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 添加一个有序集合 127.0.0.1:6379> zadd age 24 xiaoming 25 xiaobai 26 xiaojiang (integer) 3 # 获取集合的元素个数 127.0.0.1:6379> zcard age (integer) 3 # 获取 xiaobai 的分数 127.0.0.1:6379> zscore age xiaobai "25" # 获取 xiaojiang 的排名 127.0.0.1:6379> zrank age xiaojiang (integer) 2 # 获取 xiaojiang 的排名,逆序 127.0.0.1:6379> zrevrank age xiaojiang (integer) 0 |
除了上面的几个操作以外,有序集合还提供了一些其他的 api:
|
1 2 3 4 5 6 7 |
# 返回索引在 [start, stop] 之间的元素 ZRANGE key start stop [WITHSCORES] ZREVRANGE key start stop [WITHSCORES] # 获取分数范围在 [min, max] 之间的元素 ZRANGEBYSCORE key min max [WITHSCORES] [LIMIT offset count] # 获取分数范围在 [min, max] 之间的元素个数 `ZCOUNT key min max` |
默认情况下,redis 只返回元素的 key,不会返回分数。 WITHSCORES 的作用就是在返回 key 的同时还返回分数。
1.3 增加分数
给 member 成员增加分数 increment,返回值是更改后的分数:
|
1 |
ZINCRBY key increment member |
示例:
|
1 2 |
127.0.0.1:6379> zincrby age 2 xiaojiang "28" |
1.4 根据条件删除元素
删除指定范围的元素:
|
1 2 3 4 |
# 删除排名在 [start, end] 之间的元素 ZREMRANGEBYRANK key start end # 删除分数在 [min, max] 之间的元素 ZREMRANGEBYSCORE key min max |
二、编码和原理
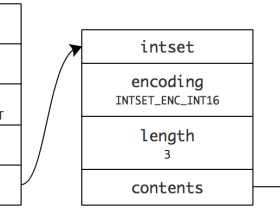
有序集合内部使用 ziplist 和 skiplist 来编码,当集合满足下面两个条件时,对象使用 ziplist,否则使用 skiplist 。
- 集合的元素个数小于 128
- 所有元素的长度小于 64
当条件不足时,redis 会自动转换编码。一个转换示例:
|
1 2 3 4 5 6 7 8 9 10 |
127.0.0.1:6379> zadd age 10 nginx (integer) 1 127.0.0.1:6379> object encoding age "ziplist" # 添加一个长度超过 64 的 key,... 是省略的 60 个字符 127.0.0.1:6379> zadd age 10 wwwwwww...wwwwwwww (integer) 1 # 编码转换成 skiplist 127.0.0.1:6379> object encoding age "skiplist" |
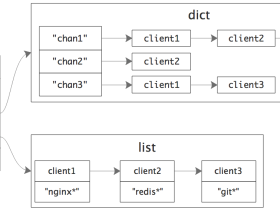
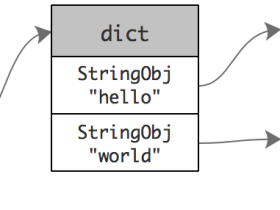
除了用链表以外,有序集合还是用了哈希表作为底层实现之一。哈希表保存了所有节点和分数的对应关系,它的作用主要是方便定位元素位置,在 O(1) 的时间内找到元素。否则,根据跳跃表的特性,需要 (logN) 的时间才能找到数据,对于集合而言效率太低了。
字典里面保存了所有节点和分数的对应关系,但是所有的对象节点并不是额外再创建的,它是直接用的跳跃表中元素的节点,这样避免了占用额外空间,二来还可以直接定位到对应节点地址,方便修改。
有序集合内部结构图如图所示:
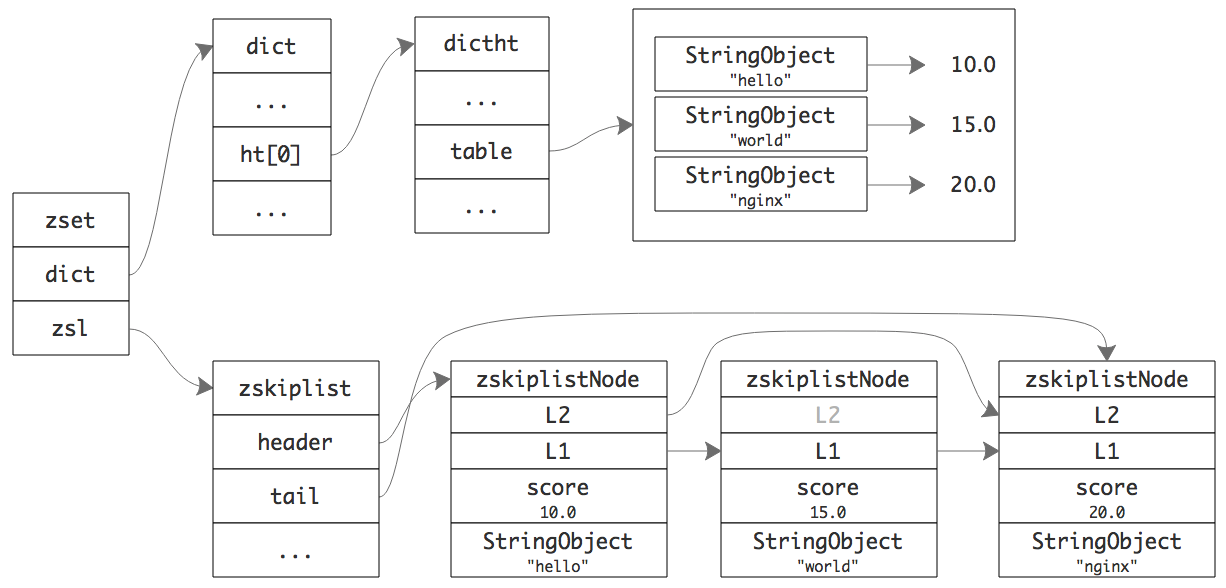




评论