来源:力扣 (LeetCode)
链接:https://leetcode-cn.com/problems/add-two-numbers
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
一、题目描述
给出两个非空的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储一位数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例:
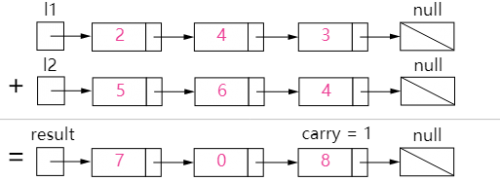
- 输入:(2 -> 4 -> 3) + (5 -> 6 -> 4)
- 输出:7 -> 0 -> 8
- 原因:342 + 465 = 807
二、题解
思路:
我们使用变量来跟踪进位,并从包含最低有效位的表头开始模拟逐位相加的过程。:
算法:
就像你在纸上计算两个数字的和那样,我们首先从最低有效位也就是列表 l1 和 l2 的表头开始相加。由于每位数字都应当处 [0, 9] 的范围内,我们计算两个数字的和时可能会出现 「溢出」 。例如,5 + 7 = 12 。在这种情况下,我们会将当前位的数值设置为 2,并将进位 carry = 1 带入下一次迭代。进位 carry 必定是 0 或 1,这是因为两个数字相加 (考虑到进位) 可能出现的最大和为 9 + 9 + 1 = 19 。
伪代码如下:
- 将当前结点初始化为返回列表的哑结点。
- 将进位 carry 初始化为 00 。
- 将 p 和 q 分别初始化为列表 l1 和 l2 的头部。
- 遍历列表 l1 和 l2 直至到达它们的尾端。
- 将 x 设为结点 p 的值。如果 p 已经到达 l1 的末尾,则将其值设置为 0 。
- 将 y 设为结点 q 的值。如果 q 已经到达 l2l2 的末尾,则将其值设置为 0 。
- 设定 sum = x + y + carry 。
- 更新进位的值,carry = sum / 10 。
- 创建一个数值为 (sum % 10) 的新结点,并将其设置为当前结点的下一个结点,然后将当前结点前进到下一个结点。
- 同时,将 pp 和 qq 前进到下一个结点。
- 检查 carry = 1 是否成立,如果成立,则向返回列表追加一个含有数字 11 的新结点。
- 返回哑结点的下一个结点。
请注意,我们使用哑结点来简化代码。如果没有哑结点,则必须编写额外的条件语句来初始化表头的值。
特别注意以下情况:
- 当一个列表比另一个列表长时
- 当一个列表为空时,即出现空列表
- 求和运算最后可能出现额外的进位,这一点很容易被遗忘
三、代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode(int x) : val(x), next(NULL) {} * }; */ class Solution { public: ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) { ListNode *rs, *p, *q, *cur; int carry = 0, sum, x, y; rs = new ListNode(0); cur = rs; p = l1; q = l2; // [1] 注意循环终止的条件是两个链表都不为空了才停止 while (p || q) { // [2] 注意 p 或者 q 等于 NULL 的清情况 x = p ? p->val : 0; y = q ? q->val : 0; // [3] 注意加上进位 sum = x + y + carry; cur->next = new ListNode(sum % 10); carry = sum / 10; // [4] 注意处理 p 或 q 节点等于 NULL 的情况 p = p ? p->next : NULL; q = q ? q->next : NULL; cur = cur->next; } // [5] 注意最后的进位 if (carry) { cur->next = new ListNode(carry); } // [6] 返回 rs 的下一个节点 return rs->next; } }; |
复杂度分析:
- 时间复杂度:O(max(m,n)),假设 m 和 n 分别表示 l1 和 l2 的长度,上面的算法最多重复 max(m,n) 次。
- 空间复杂度:O(max(m,n)), 新列表的长度最多为 max(m,n)+1 。