一、二叉搜索树
1.1 什么是二叉搜索树
算法导论中对二叉搜索树 (Binary Search Tree, 简称 BST) 的定义:
设 x 是二叉搜索树中的一个节点,如果 y 是 x 左子树中的一个节点,那么 y.key<=x.key 。如果 y 是 x 右子树中的一个节点,那么 y.key>=x.key 。
以下两棵树就是二叉搜索树:
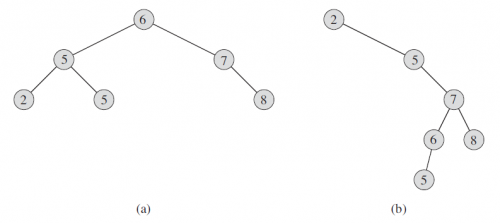
其中 a 是一个包含 6 个节点,高度为 2 的二叉搜索树。 b 是一个包含相同关键字、高度为 4 的低效二叉树。
注意:树中包含了两个相同的节点 5,在实际用途中,很少把相同的关键字放到二叉搜索树中。
二叉搜索树主要的操作:
SEARCH:查找某个节点在树中的位置MINIMUM:求以指定节点为根的树中的最小元素MAXIMUM:求以指定节点为根的树中的最大元素PREDECESSOR:求指定节点的前驱节点SUCCESSOR:求指定节点的后继节点INSERT:在树中插入节点DELETE:删除节点
定理:二叉搜索树中的以上各个操作都是在 O(h)时间内完成。
1.2 树节点定义
二叉搜索树的节点需要包含以下元素:
- 节点的键值,也就是 key
- 父节点和左右子节点的指针
假设 key 值类型为 int,那么树节点的结构应该为:
|
1 2 3 4 5 6 |
struct bst_tree_node_st { int key; struct bst_tree_node_st *lchild; struct bst_tree_node_st *rchild; struct bst_tree_node_st *parent; }; |
二、二叉树操作
2.1 查找操作 ( SEARCH)
通过二叉搜索树的性质很容易得到查找算法:从树根开始查找,沿着树的路径一直向下。对每个遇到的节点 x,比较关键字 k 和 x.key,如果两个关键字相等,查找终止。如果 k 小于 x.key,在 x 的左子树中继续查找。否则就在 x 的右子树中继续查找。
伪代码如下 (来自 《算法导论》):
|
1 2 3 4 5 6 |
TREE-SEARCH(x, k) if x == NIL or k == x.key return x if k < x.key return TREE-SEARCH(x.left, k) else return TREE-SEARCH(x.right, k) |
上面采用了递归的方法来进行查找,递归最明显的特点就是简单,代码量小。但是在树高度很高时候,递归就会产生巨大的内存消耗和更多的 CPU 消耗,因为要频繁对函数及参数压栈,并且函数中栈是有大小限制的,不能无限递归。
大部分时候建议使用非递归查找,非递归查找的伪代码实现为:
|
1 2 3 4 5 6 |
ITERATIVE-TREE-SEARCH(x, k) while x ≠ NIL and k ≠ x.key if k < x.key x = x.left else x = x.right return x |
非递归对应的 C 语言描述:
|
1 2 3 4 5 6 7 8 9 10 |
struct bst_tree_node_st *bst_tree_search(struct bst_tree_st *t, int key) { struct bst_tree_node_st *p = t->root; while (p != NULL && key != p->key) { if (key < p->key) p = p->lchild; else p = p->rchild; } return p; } |
2.2 求最大元素 (MAXIMUM) 和最小元素 (MINIMUM)
根据二叉树的性质可知:最小的节点一定是最左边的节点,最大的节点一定是最右边的节点。
例如对下面这个二叉树而言,最小的元素是 2,最大的元素是 20 。
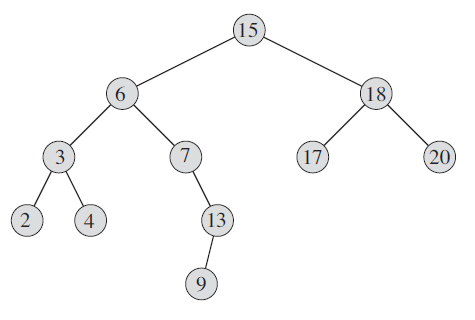
找最小的元素只要一直在左子节点中查找,直到节点的左节点是 NULL 为止。相反,找最大的元素,只要在节点的右节点中查找,直到右节点是 NULL 为止。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
/* * 得到某个子树中的最小元素节点 * @root 待查找的子树根节点 * @return 返回最小元素节点的指针,如果最小元素就是 node,那么返回 node */ struct bst_tree_node_st *bst_tree_minimum(struct bst_tree_node_st *root) { struct bst_tree_node_st *p = root; while (p != NULL && p->lchild != NULL) p = p->lchild; return p; } /* * 得到某个子树中的最大元素节点 * @root 待查找的子树根节点 * @return 返回最大元素节点的指针,如果最大的元素就是 node,那么返回 node */ struct bst_tree_node_st *bst_tree_maximum(struct bst_tree_node_st *root) { struct bst_tree_node_st *p = root; while (p != NULL && p->rchild != NULL) p = p->rchild; return p; } |
2.3 求前驱 (PREDECESSOR) 和后继 (SUCCESSOR)
节点 x 的前驱节点是指中序遍历中顺序在 x 之前的元素,节点 x 的后继节点指中序遍历中顺序在 x 之后的元素。
以 2.3 节中的二叉树为例,其中序遍历的结果为:2 3 4 6 7 9 13 15 17 18 20 。对于元素 6 而言,它的前驱节点是 4,后继节点是 7 。

求前驱节点的过程:
- 如果节点有左子节点,那么前驱节点一定是左子树中的最大元素。例如
6的前驱是4,15的前驱是13 - 如果节点没有左子节点,那么它的前驱就是以它或者以它任一祖先为右儿子的节点,例如上图中节点
9的前驱是7,节点7的前驱是6
求后继节点的过程:
- 如果节点有右子节点,那么后继节点一定是右子树中最小的元素。例如
15的后继节点是17,18的后继节点是20 - 如果节点没有右子节点,那么它的后继就是以它或者以它任一祖先为左儿子的节点,例如上图中的
13的后继节点是15,17的后继节点是18
可以得到的一个结论:树中最小的元素没有前驱节点,树中最大的元素没有后继节点。
求前驱节点和后继节点的 C 语言描述:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
/* * 求树中某个节点的后继节点 * @node 当前节点,如果没有后继节点,返回 NULL */ struct bst_tree_node_st *bst_tree_successor(struct bst_tree_node_st *node) { struct bst_tree_node_st *x = node, *p; if (x->rchild) return bst_tree_minimum(x->rchild); p = x->parent; while (p != NULL && p->rchild == x) { x = p; p = x->parent; } return p; } /* * 求树中某个节点的前驱节点 * @node 当前节点,如果没有前驱节点,返回 NULL */ struct bst_tree_node_st *bst_tree_predecessor(struct bst_tree_node_st *node) { struct bst_tree_node_st *x = node, *p; if (x->lchild) return bst_tree_maximum(x->lchild); p = x->parent; while (p != NULL && p->lchild == x) { x = p; p = p->parent; } return p; } |
2.4 插入节点 (INSERT)
插入节点和搜索节点的工作方式一样,先根据元素大小找到合适的位置,然后作为子节点插入,每次插入的节点必定是叶子节点。
例如在下面的树中插入元素 13,首先要找到它的父节点 15,然后作为它的左子节点插入:
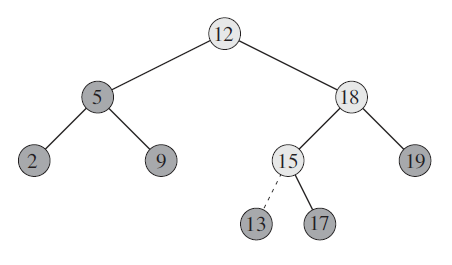
C 语言实现:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
/* * 在树中插入节点 * @t 树 * @node 新节点 */ void bst_tree_insert(struct bst_tree_st *t, struct bst_tree_node_st *node) { struct bst_tree_node_st *x, *y; y = NULL; x = t->root; // 找到合适的插入位置 while (x != NULL) { y = x; if (node->key < x->key) x = x->lchild; else x = x->rchild; } node->parent = y; if (y == NULL) t->root = node; else if (node->key < y->key) y->lchild = node; else y->rchild = node; } |
2.5 删除节点 (DELETE)
2.5.1 删除节点的基本操作
相对来说,删除节点要比插入节点复杂许多,它有三种不同的情况:
- 如果待删除节点 z 没有孩子节点,那么直接把它删除,修改父节点指针即可完成。
- 如果待删除节点 z 只有一个孩子,那么将这个孩子替换到 z 的位置,修改 z 的父节点指针,指向 z 的子节点。
- 如果待删除节点 z 有两个孩子,找到 z 的后继节点 y,让 y 占据 z 的位置,同时还要让 y 的右子节点 (如果有的话) 占据 y 的位置。
前面两种情况相对简单,甚至可以被合并成一种情况。而第三种情况最为复杂,它还能继续向下分解:
- z 的后继节点 y 就是 z 的右子节点
- z 的后继节点 y 不是 z 的右子节点,这种情况下可以推断出 y 一定不含左子节点,但此时 y 的右子节点 x 又有两种情况:
- x 为空
- x 不为空
下面分别对以上几种情况进行讨论:
2.5.2 删除节点只有一个儿子
只有左子节点的情况
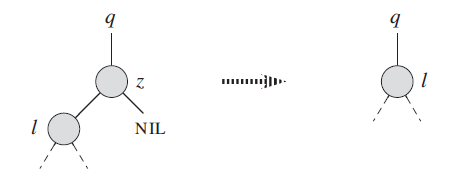
只有右子节点的情况
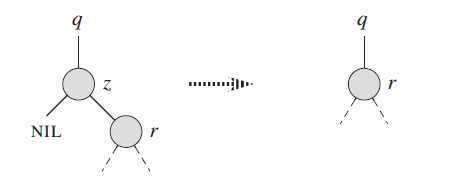
不管是左儿子,还是右儿子,直接替换原删除节点即可。
2.5.3 删除节点有两个儿子且后继节点是右儿子
对应情况:
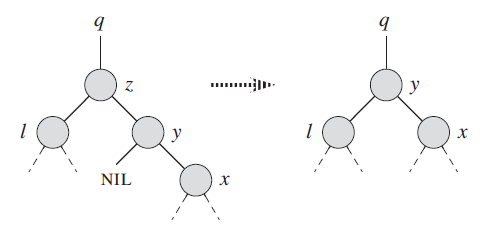
只需要把 z 的位置替换成 y 就可以了。
2.5.4 删除节点有两个儿子且后继节点不是右儿子
后继节点 y 不是 z 的右儿子,那么 y 必定没有左儿子 (如果 y 有左儿子的话,那么 z 的后继节点肯定就是 y 的左儿子而不会是 y) 。
情况对应下图:
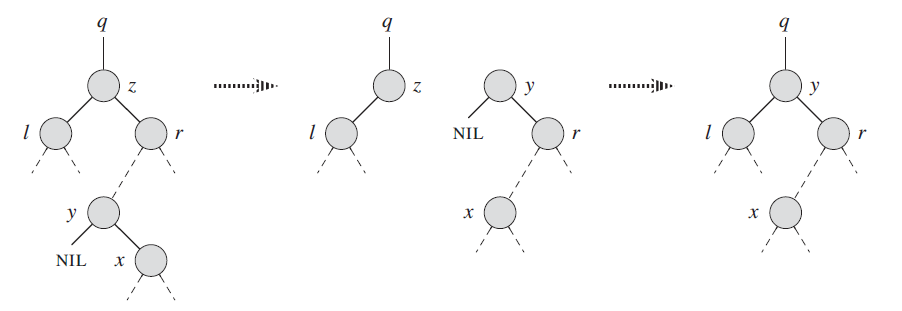
此时要做的两步操作:
- 将
y的右儿子 (不管是否为 NULL) 替换成y - 将
y替换成z
2.5.4 删除节点的代码
添加一个辅助操作 TRANSPLANT,英文意思是移植,表示把一个节点用另一个节点代替:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
static void transplant(struct bst_tree_st *t, struct bst_tree_node_st *old_node, struct bst_tree_node_st *new_node) { if (old_node->parent == NULL) t->root = new_node; else if (old_node == old_node->parent->lchild) old_node->parent->lchild = new_node; else old_node->parent->rchild = new_node; // 如果替换新节点不是 NULL,设置新节点的父指针指向 if (new_node != NULL) new_node->parent = old_node->parent; |
然后在 TREE_DELETE 操作中调用 TRANSPLANT 完成删除操作:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
/* * 删除节点 * @t 树 * @node 待删除的节点 */ void bst_tree_delete(struct bst_tree_st *t, struct bst_tree_node_st *node) { struct bst_tree_node_st *y; if (node->lchild == NULL || node->rchild == NULL) // 至少有一个子节点为空,直接用子节点替换 _transplant(t, node, node->lchild ? node->lchild : node->rchild); else { // 得到右子树中的最小节点,即节点在右子树中的后继节点 y = bst_tree_minimum(node->rchild); if (y->parent != node) { // y 不是删除节点的子节点,用 y 的右节点替换 y _transplant(t, y, y->rchild); y->rchild = node->rchild; y->rchild->parent = y; } // 用 y 替换删除节点 _transplant(t, node, y); y->lchild = node->lchild; y->lchild->parent = y; } } |