一、后序遍历
后序遍历逻辑:优先访问左、右子节点,然后访问当前节点。
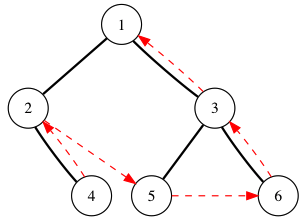
一个后序遍历的示例,它的后序遍历结果为 [4, 2, 5, 6, 3, 1]:
二、非递归实现
后序遍历的非递归实现比前序和中序的非递归实现要复杂很多,因为每个节点都可能有 2 个子节点,遍历的时候节点中并没有保存当前的状态,无法确定两个子节点是否已经访问过了。因此,下面采用两个方法来实现非递归访问。
2.1 实现方式一
通过栈+链表配合,流程如下:
- 根节点入栈,然后循环遍历访问栈顶元素。
- 每访问一个元素,把该元素插入到链表开头,然后分别把左、右子节点压栈。
- 循环 1-2 步,完成后把链表中的节点顺序输出。
代码实现:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
void postorder_traversal2(tree_node<T> *node, vector<T> &v) { stack<tree_node<T> *> s; list<tree_node<T> *> l; typename list<tree_node<T> *>::iterator it; tree_node<T> *p; if (node == nullptr) return; s.push(node); while (!s.empty()) { // 取栈顶元素 p = s.top(); s.pop; // 插入到链表的开头 l.push_front(p); // 左子树入栈 if (p->lchild) s.push(p->lchild); // 右子树入栈 if (p->rchild) s.push(p->rchild); } // 结果放到 vector 中去 while (!l.empty()) { p = l.front(); l.pop_front(); v.push_back(p->val); } } |
2.2 实现方式二
非递归的后序遍历和前、中序遍历一样,也依赖栈这个数据结构,原理:
- 把根节点压栈两次,然后循环判断,当栈不为空的时候,取出栈顶元素。
- 把取出的栈顶元素和栈当前的栈顶元素对比,如果相等,则把右子节点和左子节点也分别压入栈两次;如果不相等,则访问当前元素。
压栈两次的作用:判断第几次访问节点,第一次访问到节点的时候要先访问子节点,第二次才是访问自己。
一个特别要注意的地方是:栈是先进后出的,所以在压入左右子节点的时候,要先压入右子节点。
代码实现:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
void postorder_traversal(tree_node<T> *node, vector<T> &v) { stack<tree_node<T> *> st; tree_node<T> *p; if (node == nullptr) return; // 根元素压栈 2 次 st.push(node); st.push(node); while (!st.empty()) { // 弹出栈顶元素 p = st.top(); st.pop(); if (!st.empty() && p != st.top()) { // 如果栈顶元素和刚取出的相等,说明还没有访问过 // 先压入右子节点 if (p->rchild) { st.push(p->rchild); st.push(p->rchild); } // 再压入左子节点 if (p->lchild) { st.push(p->lchild); st.push(p->lchild); } } else { // 已经访问过了 v.push_back(p->data); } } } |
三、递归实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
/* * 后序遍历的递归实现 * @node 需要遍历的节点 * @v 保存遍历结果的数组 */ void postorder_traversal(tree_node<T> *node, vector<T> &v) { if (node == nullptr) return; if (node->lchild) postorder_traversal(node->lchild); if (node->rchild) postorder_traversal(node->rchild); v.push_back(node->data); } |