53-最大子序和

来源：力扣 （LeetCode）

链接：https://leetcode-cn.com/problems/maximum-subarray/

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

一、题目描述

给定一个整数数组 nums ，找到一个具有最大和的连续子数组 （子数组最少包含一个元素），返回其最大和。

示例:

• 输入：[-2,1,-3,4,-1,2,1,-5,4]
• 输出：6
• 解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

进阶：

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

分治法并不能算是最优解，但是可以锻炼对该算法的掌握情况。本题不考虑此算法。

二、题解

2.1 贪心算法

算法：

1. 遍历数组，使用 sum 变量计算每一个节点时的最大和，用 ans 表示当前所有区间的最大子序和。
2. 运行到第 i 个节点的时候，如果 sum > 0，说明对当前节点有增益效果，sum 继续加上当前节点。
3. 如果 sum <= 0，说明之前的序列对当前节点来说没有增益效果，之前的和可以舍弃。 sum 从当前节点开始重新计算。
4. 然后比较 ans 和 sum 的大小，较大的赋值给 sum 。

图例：

图片来源于解答：画解算法：53. 最大子序和 ， © 著作权归作者所有 。

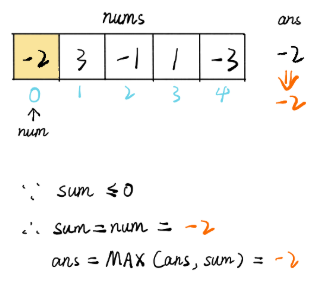
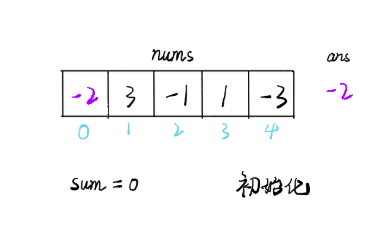
以数组 [-2, 3, -1, 1, -3] 为例，初始化时设置 sum 为 0，ans 为第一个元素的值：

访问第一个元素-2，当前 sum 为 0，更新 sum 为当前节点的值-2，sum 和 ans 对比 ans 还是-2：

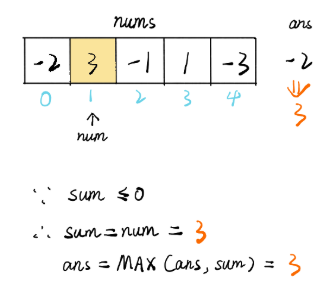
访问第二个元素 3，因为 sum = -2，如果加上当前节点，会使得连续和变成 1（还不如不加，不加是 3） 。因此重新计算 sum，设置 sum 为当前节点值 3，继续往前计算：

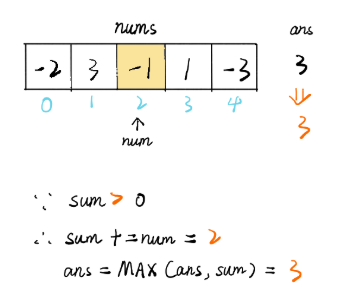
访问第三个元素-1，此时 sum > 0，对-1 有增益效果，sum 加上-1 等于 2，ans 不变：

第四个元素：

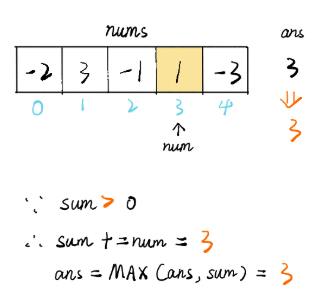
到第五个元素时，sum = 3，加上-3 之后等于 0，ans 依旧等于 3：

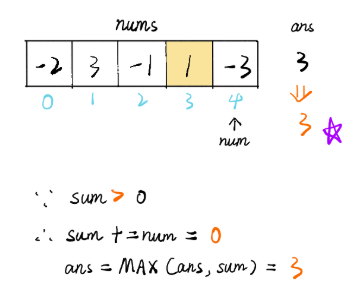
然后到此结束，最大连续和是 3 。

代码：

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

2.2 动态规划

算法：

其实动态规划的思路和上面的贪心算法差不多，关键的结果是动态规划的状态方程：假设 dp[i] 是第 i 个节点时候的最大连续和，那怎么计算它的值呢？

其实还是和上面的贪心算法一样，只要 dp[i - 1] 加上当前节点的和大于当前节点，那么 dp[i] 就等于和值。否则 dp[i] 就应该设置为当前节点值，所以它的状态转移方程是：

代码：

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)，整个状态中只用到了 dp[i] 和 dp[i - 1]，优化成 O(1) 。