数据结构之 B 树

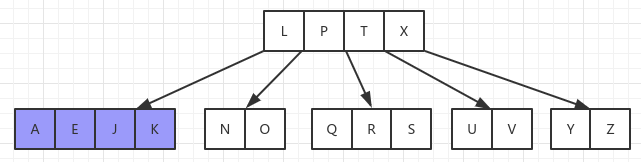
一、 B 树的基本概念

B 树是一种多叉树，被广泛应用于数据库索引中。它也是一种特殊的搜索树，和搜索树最大的不同在于它的每个节点都包含了 n 个关键字和 n+1 个指向子节点的指针。它的表现形式为：

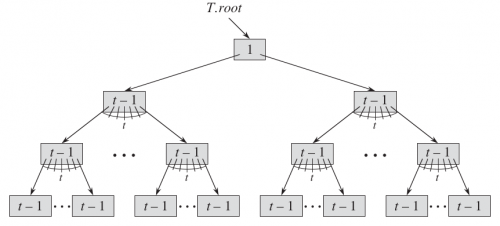
B 树的特点：

1. 假设 x.key 为当前节点中的关键字，x.child.key 是子节点中的关键字，那么它们之间存在以下关系：
   x.child.key <= x.key1 <= x.child2.key <= x.key2 <= x.child3.key <= ... <= x.keyn
2. 每个节点的关键字个数都有上界和下界，上下界用 B 树的最小度数 t ≥ 2 来表示。
3. 除了根节点以外，每个节点必须有 t - 1 个关键字，除了根节点以外，每个节点都有 t 个孩子。
4. 每个节点最多有 2t - 1 个关键字，最多有 2t 个孩子。当一个节点恰好有 2t - 1 个关键字时，称该节点是满的。
5. t = 2 的时候 B 树最简单，每个内部节点有 2 、 3 或者 3 个孩子，也被称作 2-3-4 树。
6. t 值越大，B 的高度就越小。

为什么 B 树广泛应用于索引中

因为磁盘读取的最小单位是扇区，每个扇区是 512 字节。操作系统读取磁盘的最小单位是块，一个块包含了若干个扇区 （一般一个块是 4096 字节，包含 8 个扇区） 。如果和红黑树或其他二叉搜索树一样，每个节点只保存一个数据，那么磁盘读取的效率就相当低了。如果需要读取多个数据，就要执行多次磁盘 IO 操作才能完成任务了，而磁盘 IO 在系统中属于较为耗时的操作，因此多次 IO 势必导致效率大大降低。

B 树就是为了改进这一问题而衍生出来的，B 树的节点一般设置为磁盘的块大小，也就是 4K，里面包含了多个数据节点的内容，这样一次 IO 就能读到多个数据内容。并且由于 B 树也具有搜索树的性质，因此很快就能定位到数据内容。

二、 B 树操作

B 树的主要操作有两个：分裂和合并。因为 B 树的每个节点包含关键字的数量为 [t - 1, 2t - 1]，当节点的关键字数量超出后，就要对节点进行分裂操作，分裂操作会导致 B 树高度增加。当节点关键字被删除，数量不满足条件时就要合并两个节点，合并节点会导致 B 树高度下降。

3.1 增加节点

以一个度为 4 的 B 树为例，插入 S 后，B 树节点的关键字数量变成了 7，需要进行分裂。

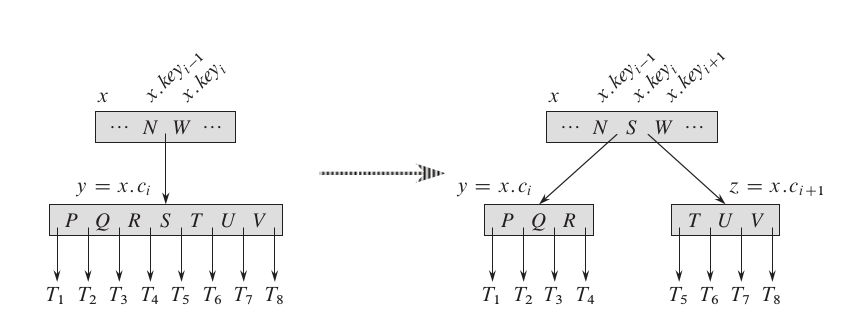
此时对节点的分裂过程为：

1. 新生成节点，将 S 右边的关键字和子节点移到新节点中。
2. S 左边的关键字和子节点保存在当前节点。
3. S 节点往上提，放到父节点中的合适位置。
4. 如果 S 节点上提导致父节点的数量也超出了，还需要继续对父节点进行分裂。

注意：每次上提到父亲节点的关键字都是被分裂节点的中间关键字。

分裂示例

以下是度为 3 的 B 树分裂的过程，每个节点最多有 5 个关键字，最少 2 个关键字。

初始时的 B 树：

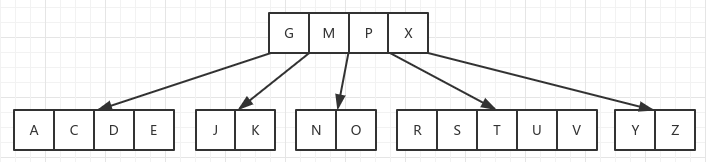
插入 B，这只是一个简单的对叶节点插入的过程，插入后不会影响其他节点，B 树的条件也还满足，直接插入就行：

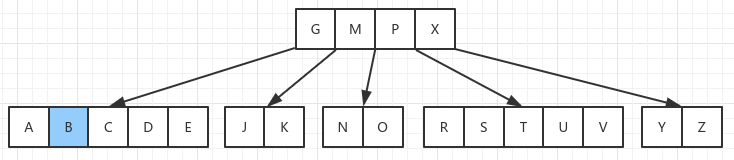
插入 Q，因为插入 Q 后会导致 RSTUV 节点关键字超出，因此要分裂这个节点。 T 节点作为中间节点放到父节点中 （也可以把 S 提到父节点，T 放在 UV 节点）：

插入 L，它被放到 JK 节点之后，也是一个简单的叶节点插入。但是因为根节点的关键字满了，所以对根节点分裂，此时将 P 提出来作为根节点，树的高度加 1：

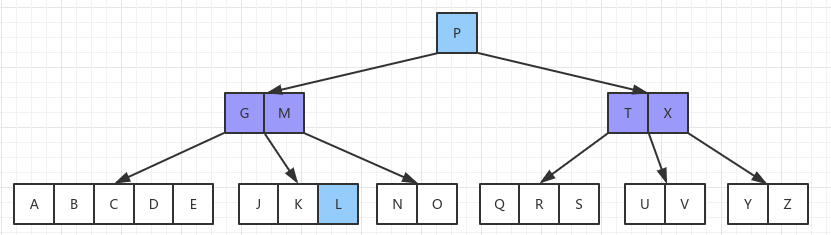
插入 F，放在 ABCDE 节点之后，插入后将导致节点分裂，节点 C 提到父节点：

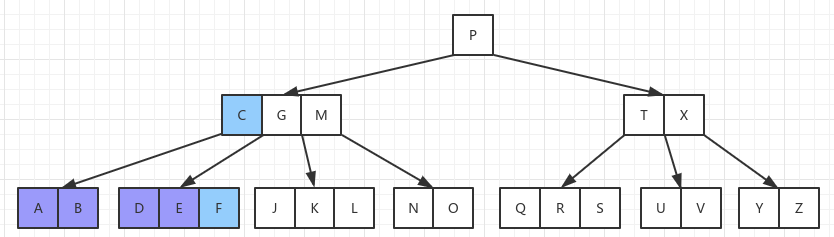
2.3 删除节点

在 B 树中删除节点，将会引发节点的合并。相对于增加节点来说，删除节点的远比增加节点要复杂。

以上面的 B 树为例，初始状态为：

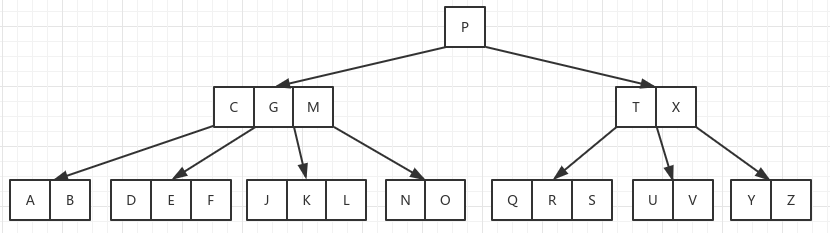
删除关键字 F，作为叶子节点，删除 F 后并没有影响到 B 树的性质，直接删除即可。得到以下 B 树：

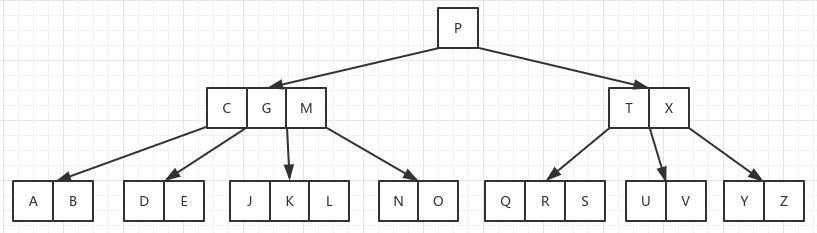
删除关键字 M，因为 M 所处的节点是内部节点，删除 M 后会导致 NO 关键字所在的节点没有父节点。此时需要把 M 的前驱关键字 L 替换掉 M，然后删掉 L：

也可以把 M 的后继关键字 N 替换上来，但是 M 替换后会导致子节点不满足关键字数量条件。

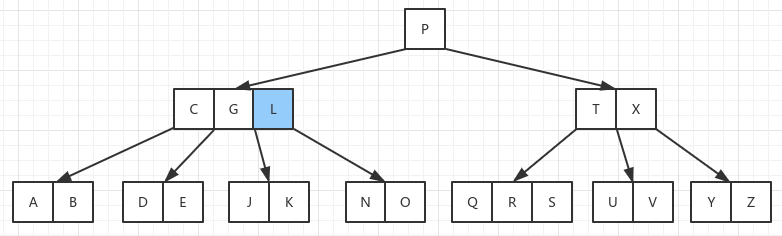
删除关键字 G，G 所处的节点也是内部节点，删除后会导致 DE 或者 JK 所处的节点没有父节点，此时也需要和上面删除 M 一样在子节点中找到前驱或者后继替换上来。但是这里不同的是，两个子节点都是只有 t - 1 个关键字，再从中拿掉一个关键字后会导致子节点关键字数量不满足。此时就需要合并两个子节点，然后直接删除 G 节点：

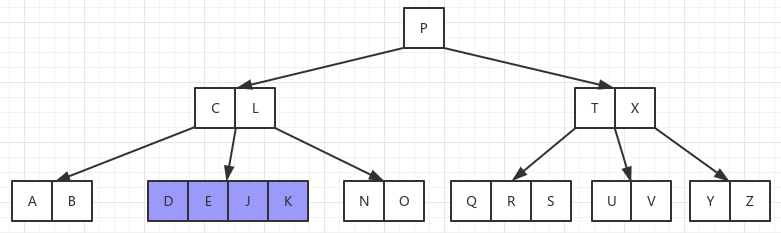
删除关键字 D，D 所处的节点是叶子节点，可以和删除节点 F 一样，直接删除。但是这里也有一个不同的点是，父节点和父节点的兄弟节点此时都只有 t - 1 个节点，此时除了删除节点 D 以外，还要合并父亲节点，此时树的高度减一：

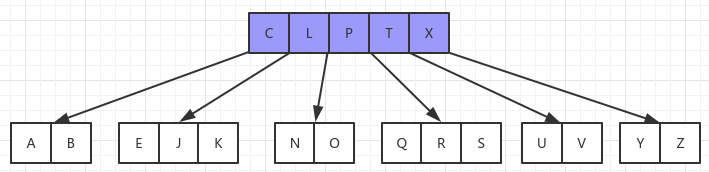
删除关键字 B，B 所在的节点关键字数量是 t - 1，删除 B 后会导致节点的最小关键字数量不满足条件。因此要从父节点或者兄弟节点借一个关键字。此时就分为两种情况：

1. 如果兄弟节点的关键字个数也是 t - 1，那么直接和兄弟节点合并，从父节点提取一个关键字下来 （下面删除 C 时候的场景） 。
2. 如果兄弟节点的关键字个数大于 t - 1（目前就是这个情况，兄弟节点有 3 个关键字），此时就从父节点借一个关键字 C 替换掉 B，借掉 C 后，就相当于删除了一个内置节点的元素，所以父亲节点要从它后继节点中找一个关键字补上，也就是 E 。最终的结果就是用 C 覆盖 B，再用 E 覆盖原来 C 的位置，再删除 E 。

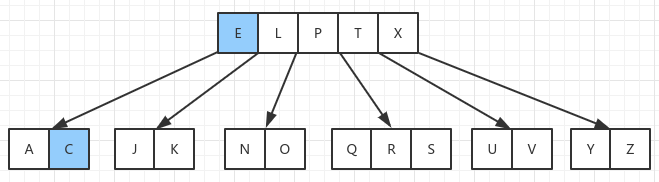
删除节点 C，此时的情况就是上面的第一种情况了，兄弟节点的关键字个数是 t - 1，要合并两个节点，得到：