本篇文章是基于前篇 《数据结构之链表 (一):单向链表》 实现的,和单向链表重复的细节不再描述。
一、双向链表
双向链表和单向链表类似,唯一的区别是链表节点中除了有指向下一个节点的指针以外,还有一个指向上一个节点的指针。

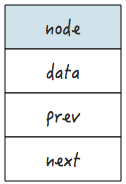
节点的定义:
|
1 2 3 4 5 6 7 8 9 |
template<typename T> class list_node { public: friend class doubly_linkedlist<T>; private: T data; list_node<T> *prev; // 指向前一个节点 list_node<T> *next; // 指向后一个节点 }; |
链表的定义:
|
1 2 3 4 5 6 7 8 9 |
template<typename T> class doubly_linkedlist { public: doubly_linkedlist() : head(nullptr), tail(nullptr), len(0) {} private: size_t len; // 链表长度 list_node<T> *head; // 头节点 list_node<T> *tail; // 尾结点 }; |
二、插入操作
双链表的插入操作和单链表基本没有差别,就只是多了一个修改 prev 节点的步骤。
以下是添加节点 node2 的过程:
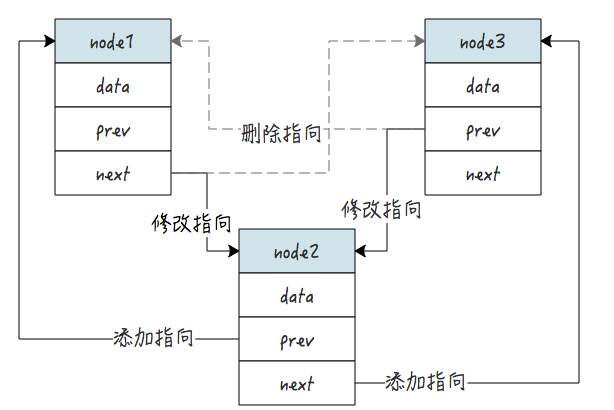
操作主要有两步:
- 修改 node2 的 prev 和 next 指向,分别指向前后节点。
- 修改前节点 node1 的 next 指针指向 node2,修改后节点 node2 的 prev 指针指向 node2 。
插入函数实现:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
/* * 添加节点操作 * @new_node 新节点,不为空 * @prev 前驱节点 * @next 后继节点 */ void add_node(list_node<T> *new_node, list_node<T> *prev, list_node<T> *next) { if (new_node == nullptr) return; len++; new_node->next = next; new_node->prev = prev; if (prev) { prev->next = new_node; } if (next) { next->prev = new_node; } } |
实现了这个函数之后,单链表中所有的头插、尾插函数都不用修改了,直接调用这个函数就完成了。
其实后面的删除元素也是一样,前面所说的把添加和删除逻辑抽离出来的好处就在这里。
三、删除操作
删除 node2 节点的操作步骤:
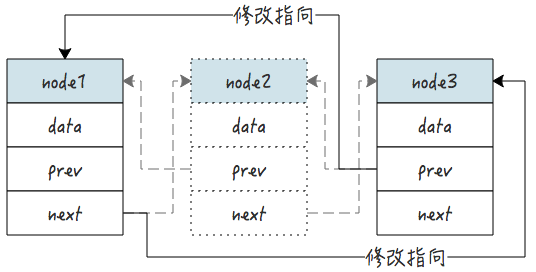
过程描述:
- 删除 node2 的 prev 和 next 指针指向。
- 修改 node1 的 next 指针指向 node3,修改 node3 的 prev 指针指向 node1 。
删除代码实现:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
void remove_node(list_node<T> *del_node, list_node<T> *prev, list_node<T> *next) { len--; del_node->next = nullptr; del_node->prev = nullptr; if (prev) { prev->next = next; } if (next) { next->prev = prev; } } |
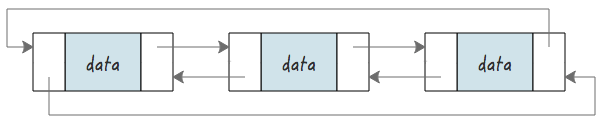
四、双向循环链表
双向循环链表是在双向链表的基础上增加了循环机制,即链表的尾结点要连接上首节点,链表的首节点要连接上尾结点。循环链表的示意图:
《算法导论》 中实现双向循环链表的方法是引入一个哨兵节点,这个节点不包含任何数据信息,只作为首尾相连的用途:

实际上也就是一个 NULL 值,和双向链表没有很大区别。