一、先序遍历
先序遍历的意思是:先遍历当前节点,再分别遍历左、右子节点。
例如一棵二叉树为:
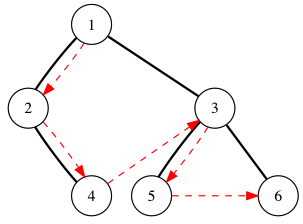
它的先序遍历序列 (红色虚线标出来的) 为:[1, 2, 4, 3, 5 6] 。
二、递归实现
递归的实现很简单,先访问当前节点,然后分别递归访问左右子节点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
/* * 先序遍历的递归实现 * @node 需要遍历的节点 * @v 保存遍历结果的数组 */ void pre_order_traversal(tree_node<T> *node, vector<T> &v) { if (node == nullptr) return; // 遍历当前节点 v.push_back(node->data); // 遍历左子树 if (node->lchild) pre_order_traversal(node->lchild); // 遍历右子树 if (node->rchild) pre_order_traversal(node->rchild); } |
三、非递归实现
非递归的方式依赖栈来实现,逻辑:
- 访问根节点,把当前节点压栈。然后设置当前节点为左子节点,重复过程,直到左子节点为空。
- 设置当前节点为栈顶节点的右子节点,重复 1 过程。
3.1 图文描述
以上面的二叉树为例,首先访问根元素 1,压栈:
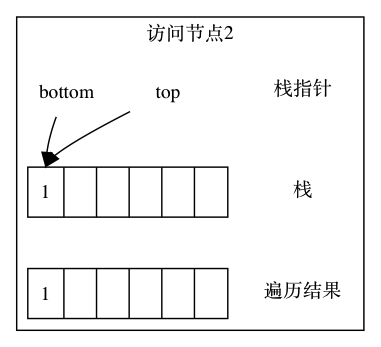
然后继续访问 1 节点的左节点 2,压栈:
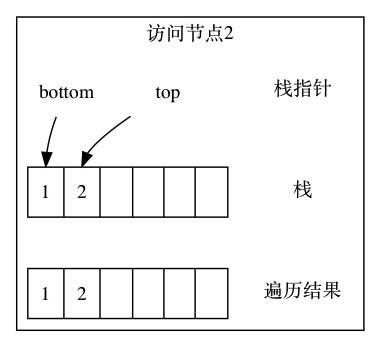
节点 2 没有左子节点,退出左树遍历。然后取出栈顶元素 2,访问它的右子节点 4:
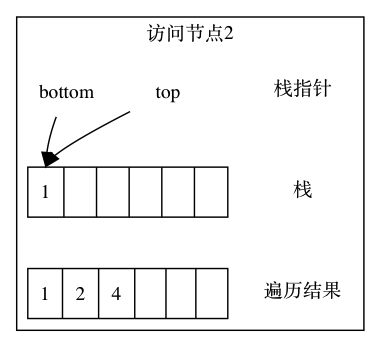
右子节点没有子节点,因此继续从栈顶取元素 1,访问它的右子节点 3 并压栈:
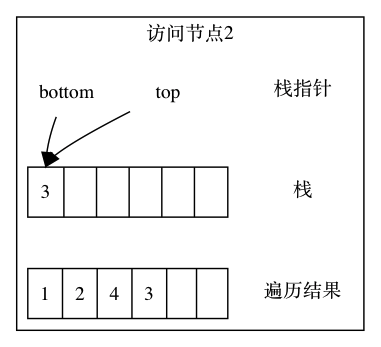
节点 3 有左子节点,顺着遍历左子节点 5,节点 5 入栈:
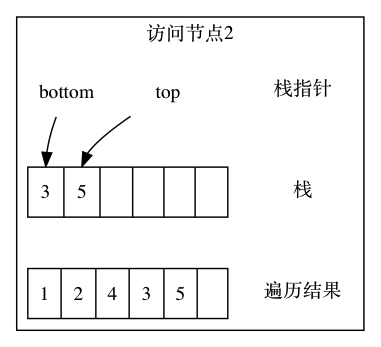
此时 5 没有没有左子节点了,于是取出栈顶元素 5,访问它的右子节点。但是它没有右子节点,继续取出栈顶元素 3,访问它的右子节点 6:
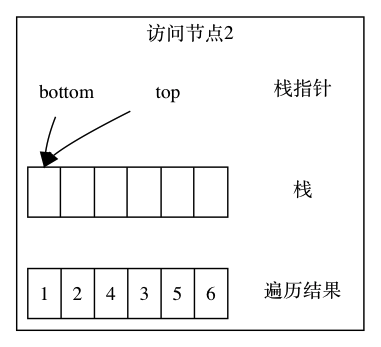
访问完 6 后,因为没有子节点了。所以继续从栈里取元素,但是此时栈也为空了,遍历结束。
3.2 代码描述
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
/* * 先序遍历的非递归实现 * @node 需要遍历的节点 * @v 保存遍历结果的数组 */ void pre_order_traversal(tree_node<T> *root, vector<T> &v) { stack<tree_node<T> *> st; tree_node<T> *p; p = root; while (p != nullptr || !st.empty()) { // 遍历左子树 while (p) { // 访问当前节点 v.push_back(p->data); // 当前节点入栈 st.push(p); // 遍历左子节点 p = p->lchild; } // 取栈顶元素,访问父亲节点的右子节点 if (!st.empty()) { p = st.top()->rchild; st.pop(); } } } |