排序算法六：快速排序

2018年3月3日20:53:14数据结构和算法评论723字数 1102阅读3分40秒阅读模式

一、原理

选择排序的原理是分治，把排序序列切分成若干个小组后分别排序。每次排序都以随机的一个元素作为哨兵（一般都以排序区间的中间元素或者首元素作为哨兵），比他大的元素都放到右边，比它小的都放到左边。然后分别对该元素左边和右边的元素再法排序，直到所有的元素都是有序状态。

具体的排序过程描述为：

选取一个哨兵元素temp，设置两个指针low和high分别从数组的两端开始遍历。
high指针从右到左遍历，当遇到A[high] < temp的时候，设置A[left]的值为A[high]。
low指针从左到右遍历，当遇到A[high] > temp的时候，设置A[high]的值为A[left]。
重复执行2、3步，直到low和high相遇，设置low元素的值为temp。此时low左边的元素都小于temp，low右边的元素都大于temp。再分别对左右子区间的元素分别排序。

图例：

以数组[54, 15, 34, 82, 15, 46, 85, 43]为例，初始状态时设置low指针指向第一个元素，high指针指向最后一个元素，temp为第一个元素的值54：

排序算法六：快速排序-图片1

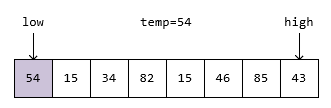
遍历high指针，从右到左找到第一个小于54的元素43，赋值给low：

排序算法六：快速排序-图片2

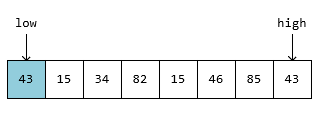
遍历low指针，从左到右找到第一个大于54的元素82，赋值给high：

排序算法六：快速排序-图片3

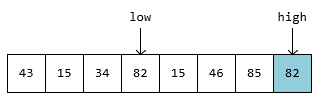
遍历high指针，从右到左找到一个小于54的元素46，赋值给low：

排序算法六：快速排序-图片4

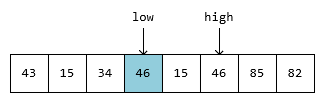
遍历low指针，继续寻找第一个大于54的元素。但是直到遇见high指针，都没有找到再比54大的元素，把temp值赋值给low：

排序算法六：快速排序-图片5

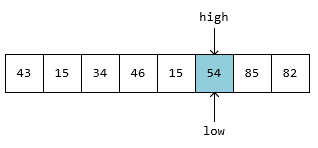
此时第一轮排序完成，54左边的元素都比它小，右边的元素都比它大。因此按照这个操作，继续对左边和右边的区间再执行相同的操作，多次排序即可完成整个数组的排序。

复杂度分析：

最坏的情况下，数组无序，快速排序和冒泡排序差不多。

时间复杂度：最坏情况下，时间复杂度为O( $n^{2}$ )；最好的情况和平均情况下算法复杂度为O( $n \log (n)$ )。
空间复杂度：最坏情况下，空间复杂度为O( $n$ )；平均情况下空间复杂度为O( $\log (n)$ )。

二、代码实现

快排的写法多样，以下实现了C++和Python两种语言的快速排序算法实现。

其中C++选取的哨兵是数组第一个元素，python选取的哨兵是数组中间元素。

2.1 C++实现

以区间中点作为排序标杆：

/*
 * 快速排序算法实现，对[left, right)部分的数组排序。
 * @data 待排序数组
 * @left 左区间，包含该下标元素
 * @right 右区间，不包含该下标元素
 */
template<typename T>
void quick_sort(vector<T> &data, int left, int right) {
    int i = left, j = right - 1;
    T temp;

    if (right <= left) {
        return;
    }

    temp = data[i];

    while (i < j) {
        // 从右到左遍历找到一个比temp小的
        while (i < j && data[j] >= temp) {
            j--;
        }
        if (i < j && data[j] < temp) {
            data[i] = data[j];
        }

        // 从左到右遍历找到一个比temp大的
        while (i < j && data[i] <= temp) {
            i++;
        }
        if (i < j && data[i] > temp) {
            data[j] = data[i];
        }
    }

    data[i] = temp;

    // 排序的区间是左闭右开
    quick_sort(data, left, i);
    quick_sort(data, i + 1, right);
}

* 快速排序算法实现，对[left, right)部分的数组排序。

* @data 待排序数组

* @left 左区间，包含该下标元素

* @right 右区间，不包含该下标元素

template<typename T>

void quick_sort(vector<T> &data, int left, int right) {

int i = left, j = right - 1;

T temp;

if (right <= left) {

return;

}

temp = data[i];

while (i < j) {

// 从右到左遍历找到一个比temp小的

while (i < j && data[j] >= temp) {

j--;

}

if (i < j && data[j] < temp) {

data[i] = data[j];

}

// 从左到右遍历找到一个比temp大的

while (i < j && data[i] <= temp) {

i++;

}

if (i < j && data[i] > temp) {

data[j] = data[i];

}

data[i] = temp;

// 排序的区间是左闭右开

quick_sort(data, left, i);

quick_sort(data, i + 1, right);

}

2.2 python

以区间中点元素作为标杆：

import math


def quick_sort(data, left, right):
    """
    快速排序算法，对[left, right)区间的元素排序
    :param data: 待排序数组
    :param left: 待排序数组的左区间，包含对对该下标元素排序
    :param right: 待排序数组的右区间，不包含对该下标元素排序
    :return:
    """
    i, j = left, right - 1

    if i >= j:
        return

    # 选择区间中点元素作为哨兵
    mid = math.floor((i + j) / 2)
    temp = data[mid]
    data[i], data[mid] = data[mid], data[i]

    while i < j:
        while i < j and data[j] >= temp:
            j -= 1
        if i < j and data[j] < temp:
            data[i] = data[j]

        while i < j and data[i] <= temp:
            i += 1
        if i < j and data[i] > temp:
            data[j] = data[i]

    data[i] = temp

    quick_sort(data, left, i)
    quick_sort(data, i + 1, right)

import math

def quick_sort(data, left, right):

"""

快速排序算法，对[left, right)区间的元素排序

:param data: 待排序数组

:param left: 待排序数组的左区间，包含对对该下标元素排序

:param right: 待排序数组的右区间，不包含对该下标元素排序

:return:

"""

i, j = left, right - 1

if i >= j:

return

# 选择区间中点元素作为哨兵

mid = math.floor((i + j) / 2)

temp = data[mid]

data[i], data[mid] = data[mid], data[i]

while i < j:

while i < j and data[j] >= temp:

j -= 1

if i < j and data[j] < temp:

data[i] = data[j]

while i < j and data[i] <= temp:

i += 1

if i < j and data[i] > temp:

data[j] = data[i]

data[i] = temp

quick_sort(data, left, i)

quick_sort(data, i + 1, right)

2.3 golang实现快速排序

2020-02-29刷leetcode添加，使用数组中间元素作为哨兵：

/*
 * 快速排序，对[left, right]区间内的元素排序
 * @nums 排序数组
 * @left 左边界
 * @right 右边界，包含该下标元素
 */
func doQuickSort(nums []int, left, right int) {
    i, j := left, right
    if left >= right {
        return
    }

    // 取中间元素作为哨兵
    mid := (i + j) / 2
    x := nums[mid]
    nums[mid], nums[i] = nums[i], nums[mid]

    for i < j {
        for nums[j] >= x && i < j {
            j -= 1
        }
        if i < j && nums[j] < x {
            nums[i] = nums[j]
        }
        for nums[i] <= x && i < j {
            i += 1
        }
        if i < j && nums[i] > x {
            nums[j] = nums[i]
        }
    }
    nums[i] = x
    doQuickSort(nums, left, i-1)
    doQuickSort(nums, i+1, right)
}

func quickSort(nums []int) []int {
    doQuickSort(nums, 0, len(nums)-1)
    return nums
}