排序算法五：堆排序

马谦马谦马谦

615
文章

17
评论

2019年4月27日12:10:54数据结构和算法评论288字数 447阅读1分29秒阅读模式

一、堆排序原理

通过最大堆的性质可以知道：一个堆中最大的元素总是在堆顶的，即数组下标0的位置。基于这一点，我们可以每次都把堆中的最大值提取出来，放到当前数组的后面。然后重新构建最大堆，重复这个过程，以此来完成一个数组的排序。

例如，一个已知的最大堆为：

排序算法五：堆排序-图片1

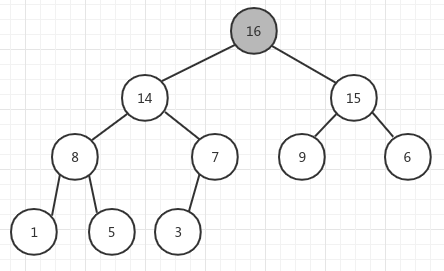
把最大的元素16提取出来，放到最后。然后重新建堆，此时堆中最大的元素为15，更新后的堆为：

排序算法五：堆排序-图片2

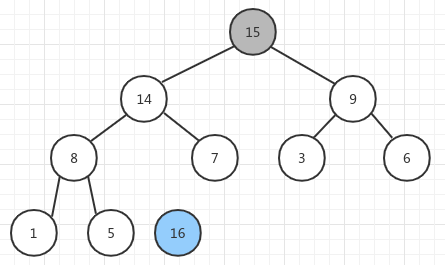
再把15提取出来，重新建堆，得到：

排序算法五：堆排序-图片3

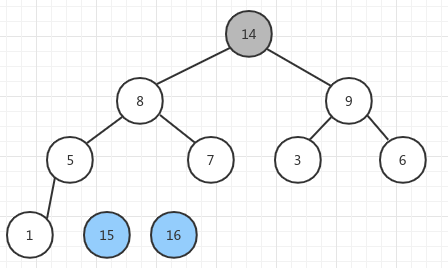
如此往复，直到最后堆中的元素只有一个，就完成了整个数组的排序。

二、代码实现

堆排序的关键点在于构造堆，如何构造堆可参考数据结构之堆。基于模板的最大堆化函数实现：

template <typename T>
static void max_heapify(T *data, size_t len, size_t idx) {
    size_t largest, lchild, rchild;

    lchild = LCHILD(idx);
    rchild = RCHILD(idx);

    if (lchild < len && data[lchild] > data[idx])
        largest = lchild;
    else
        largest = idx;

    if (rchild < len && data[rchild] > data[largest])
        largest = rchild;

    if (idx != largest) {
        my_swap(data[idx], data[largest]);
        max_heapify(data, len, largest);
    }
}

template <typename T>

static void max_heapify(T *data, size_t len, size_t idx) {

size_t largest, lchild, rchild;

lchild = LCHILD(idx);

rchild = RCHILD(idx);

if (lchild < len && data[lchild] > data[idx])

largest = lchild;

else

largest = idx;

if (rchild < len && data[rchild] > data[largest])

largest = rchild;

if (idx != largest) {

my_swap(data[idx], data[largest]);

max_heapify(data, len, largest);

}

实现堆排序，堆排序的关键点在于从后往前排：

template <typename T>
static void heap_sort(T *data, size_t len) {
    size_t i, mid;
    mid = len / 2;

    // 建堆
    for (i = mid - 1; i >= 0 && i < len; i--) {
        max_heapify(data, len, i);
    }

    // 堆排序，从后往前
    for (i = len - 1; i >= 1; i--) {
        my_swap(data[i], data[0]);
        max_heapify(data, --len, 0);
    }
}