一、计数排序
其基本思想为:假设 n 个输入的元素中的每一个都是在 0 到 k 之间的一个整数,对于每一个输入元素 x,确定小于 x 的元素个数,直接把 x 放在它输出的数组中的位置上。例如有 17 个元素小于 x,则 x 就应该在数组的第 18 个位置上。当有几个元素相同时,这一方案就要略作修改,不能都放在同一个位置上。
计数排序需要提供两个辅助数组用来计数,一个用来保存已经排好序的元素,一个用来保存每个元素在数组中出现的次数。计数排序是不稳定的排序算法,时间复杂度 (n),空间复杂度是 O(n + k),其中 k 是排序数组元素的范围。
例如以下数组 A:

在通过计数后,得到的辅助数组 C 为:
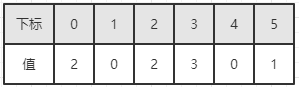
对于元素 1 而言,它前面有两个 0,因此排序后它的位置在第三个,即下标为 2 的位置上,但是它的数量为 0,就不应该给他排序。而元素 2 是有的,它的位置应该是 0 的数量和 1 的数量 (如果有元素 1 的话) 之和的后面一位,在这里是第 3 位,下标为 2 。这里类似斐波那契数列:每个元素都等于前面两个的和。
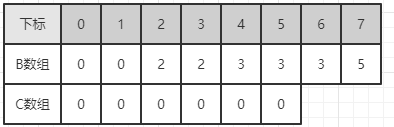
因此,有必要对辅助数组 C 做处理,设置其所在的位置为前面所有元素数量之和,这样就不用每次都重新计算前面的数量了 (参考斐波那契数列计算):
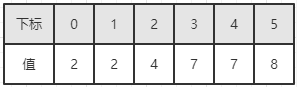
要注意的是,对于 2 这个元素来说,它出现了两次,如果不做特殊处理,它们处的位置都是第四个位置。要想办法把两个 2 分别放到自己合适的位置上去。可以采取的办法是从后往前排序,每排完一个数字,当前数字的值减一。
图例:
第一步,A 的最后一个元素是 3,得到 C[3] 的值为 7,把 3 先放到第 7 个位置,并把 C[3] 的值减一:
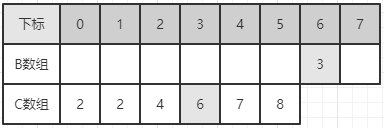
第二步,现在 A 的最后一个元素 (未排序的) 是 0,得到 C[0] 为 2,放到第二个位置,C[0] 减一:
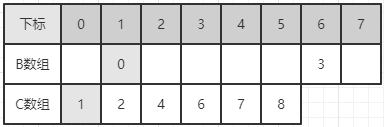
第三步,重复以上步骤,直到 A 中所有的元素都排序完毕:
此时,整个数组就是有序的了。
二、计数排序的代码实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
// 数据可能出现的最大值 const unsigned int max_val = 100; void count_sort(int data[], const unsigned int n) { // 计数数组 int cnt[max_val] = {0}; // 生成辅助数组 int *tmp = new int[n]; unsigned int i; // 初始化计数数组 for (i = 0; i < n; i++) { cnt[data[i]]++; } // 累加所有的数量 for (i = 1; i < max_val; i++) { cnt[i] += cnt[i - 1]; } // 计数排序 for (i = n - 1; i >= 0 && i < n; i--) { tmp[cnt[data[i]] - 1] = data[i]; cnt[data[i]]--; } // 拷贝辅助数组到排序数组 for (i = 0; i < n; i++) { data[i] = tmp[i]; } } |