一、单向链表
1.1 单向链表
链表是一种线性结构，通过一个链把所有的节点都链起来，因此叫做链表。它和数组最大的不同是：数组的内存是连续的，而链表不是。数组支持随机读写，但是插入和删除麻烦，链表不支持随机读写，但是插入和删除很方便。在更多场景下，链表用途更广。
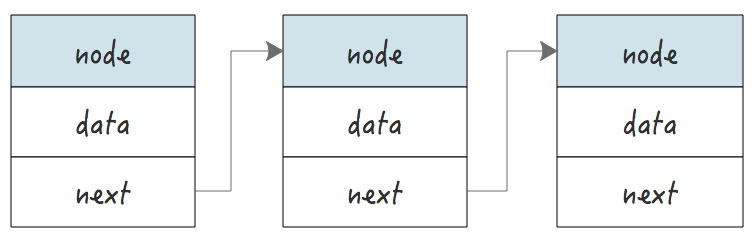
一个链表的图形示例如下，每个链表节点都包含了一个数据域和指向下一个节点指针：
链表是由一系列的节点构成，从面向对象角度来说，链表和节点是两个完全不同的东西。节点是链表中的实体，而链表只是节点的抽象，它包含若干个组成链表的节点。因此，链表和节点这两个对象应该区别开来。
一个基本的单向链表支持的操作：
- 添加节点
- 删除节点
- 查找节点
1.2 节点定义
一个节点的结构至少应该包含必要的数据域和next指针域，next只用用于指向下一个节点的地址。
以下是一个最简单的链表节点示例：
链表节点的C++定义：
|
1 2 3 4 5 6 7 8 |
template<typename T> class list_node { // 友元类，方便链表类读取节点元素数据 friend class singly_linklist<T>; private: T data; // 数据域 list_node<T> *next; // 下一个节点指针 }; |
1.3 链表定义
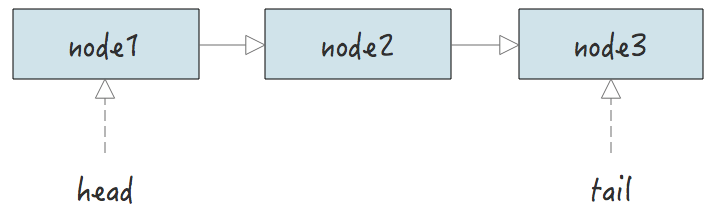
链表是由一个个的节点构成，在它的内部只要保存链表头节点的地址，就能找到链表中所有节点地址。
因此一个链表中，只要包含头结点的地址就行了。然后根据其他的扩展，我们可能还需要用到：
- 长度字段：O(1)的时间复杂度返回链表长度。
- 尾结点指针：保存末尾节点的指针，尾插时O(1)的时间复杂度即可定位到尾结点。
链表的结构示意图：
链表的C++定义：
|
1 2 3 4 5 6 7 8 9 |
template<typename T> class singly_linklist { public: singly_linklist() : len(0), head(nullptr), tail(nullptr) {} private: size_t len; // 链表长度 list_node<T> *head; // 头结点 list_node<T> *tail; // 尾结点 }; |
所有代码使用C++完成，后面的函数无特殊说明都是类成员函数。
二、插入节点
2.1 插入逻辑
以下图为例，不考虑首尾节点状态以及插入位置，一个节点被插入的逻辑是：
- 设置新增节点node2的next指向为node3
- 修改原节点node1的next指向新节点node2
- 插入完成
在链表类中，定义一个私有的添加节点函数add_node来完成这个插入操作：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
/* * 添加节点操作，新添加的节点需确保不是空值 * @new_node 新节点，不能为空 * @prev 前驱节点，可能为空 * @next 后继节点，可能为空 */ void add_node(list_node<T> *new_node, list_node<T> *prev, list_node<T> *next) { if (new_node == nullptr) return; len++; // 长度加1 new_node->next = next; if (prev) { prev->next = new_node; } } |
2.2 头插法
头插法的意思是把节点插入到链表头部，这种情况下除了插入节点到链表中，还要注意的是修改链表的head节点指针。
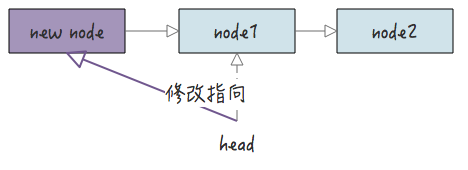
头插法函数实现：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
/* * 插入数据到链表开头 * @node 待插入的数据节点 */ singly_linklist &push_front(list_node<T> *node) { if (node == nullptr) return *this; // 添加节点到头部 add_node(node, nullptr, head); // 修改首尾节点指针 head = node; if (tail == nullptr) tail = node; return *this; } |
2.3 尾插法
尾插法和头插法相对，尾插法的意思是把节点插入到链表尾部，因此，插入后也要更新尾结点指针。
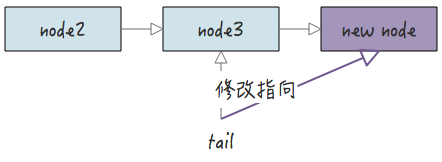
尾插法代码实现：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
/* * 插入元素到末尾 * @node 待插入的数据节点 */ singly_linklist &push_back(list_node<T> *node) { if (node == nullptr) return *this; // 插入节点到链表尾部 add_node(node, tail, nullptr); // 更新首尾结点指针 tail = node; if (head == nullptr) head = node; return *this; } |
三、查找元素
3.1 查找指定值的节点
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
/* * 在链表中查找指定值的节点 * @data 待查找节点 * @return 找到返回对应的节点，否则返回nullptr */ list_node<T> *find(const T &data) { list_node<T> *p = head; // 遍历链表 while (p) { // 找到了 if(p->data == data) return p; // 没找到，继续找下一个 p = p->next; } return p; } |
3.2 查找指定节点的前节点
在增加或删除节点之前，都要修改前节点的指针指向，因此，需要实现一个查找指定节点的头结点函数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
/* * 查找某个节点的前一个节点 * @node 当前节点 * @return 如果存在上一个节点，返回上一个节点的地址，否则返回nullptr */ list_node<T> *find_prev(list_node<T> *node) { list_node<T> *p = head; if (node == nullptr) return nullptr; while (p != nullptr) { if (p->next == node) { return p; } p = p->next; } return p; } |
四、删除元素
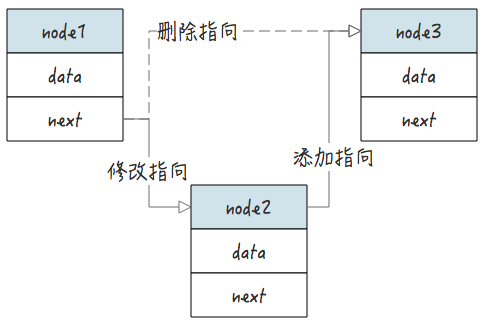
4.1 删除逻辑
以下图为例，删除节点2的操作是：
- 修改节点1的next指向node3
- 删除node2的next指向，删除完成
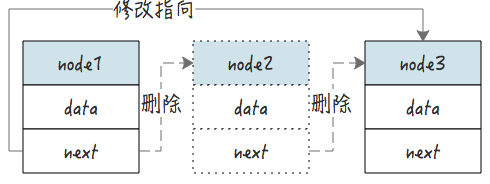
核心的删除代码：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
/* * 删除节点，待删除的节点请确保不是空值 * @del_node 待删除节点，不为空 * @prev 前驱节点，可能为空 * @next 后继节点，可能为空 */ void remove_node(list_node<T> *del_node, list_node<T> *prev, list_node<T> *next) { if (del_node == nullptr) return; len--; // 链表长度减1 del_node->next = nullptr; // 被删除节点的next指针置空 if (prev) { // prev可能为空 prev->next = next; } } |
4.2 删除指定节点
删除节点的一种操作是找到前节点指针，同时要注意的是，删除节点可能导致首尾指针失效，要注意更新首尾指针。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
/* * 删除节点 * @node 待删除节点 */ singly_linklist<T> &remove(list_node<T> *node) { list_node<T> *prev; if (node == nullptr) return *this; // 找到前节点 prev = find_prev(node); // 修改首尾节点指向 if (head == node) head = node->next; if (tail == node) tail = prev; // 删除节点 remove_node(node, prev, node->next); delete node; return *this; } |
4.3 删除首尾元素
有了上面的删除指定节点函数之后，删除首尾元素的操作就变得非常简单了：
|
1 2 3 4 5 6 7 8 |
// 弹出首元素 singly_linklist &pop_front() { return remove(head); } // 弹出尾元素 singly_linklist &pop_back() { return remove(tail); } |
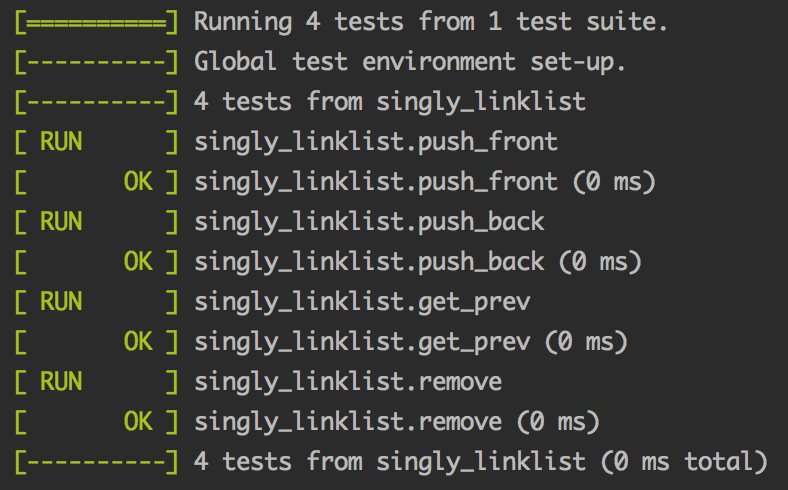
五、单元测试
5.1 头插法测试
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
TEST(singly_linklist, push_front) { int i; singly_linklist<int> list; const list_node<int> *p; vector<int> v{1, 2, 3}; list.push_front(3).push_front(2).push_front(1); EXPECT_EQ(3, list.get_len()); p = list.get_head(); for (i = 0; i < v.size(); i++) { EXPECT_EQ(p->get_data(), v[i]); p = p->get_next(); } EXPECT_EQ(p, nullptr); } |
5.2 尾插法测试
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
TEST(singly_linklist, push_back) { int i; singly_linklist<int> list; const list_node<int> *p; vector<int> v{1, 2, 3}; list.push_back(1).push_back(2).push_back(3); EXPECT_EQ(3, list.get_len()); p = list.get_head(); for (i = 0; i < v.size(); i++) { EXPECT_EQ(p->get_data(), v[i]); p = p->get_next(); } EXPECT_EQ(p, nullptr); } |
5.3 查找前一个节点测试
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
TEST(singly_linklist, get_prev) { int i; singly_linklist<int> list; const list_node<int> *p; list_node<int> *node1, *node2, *node3; // 插入3个节点 node1 = new list_node<int>(1); node2 = new list_node<int>(2); node3 = new list_node<int>(3); list.push_back(node1).push_back(node2).push_back(node3); EXPECT_EQ(3, list.get_len()); p = list.find_prev(node1); EXPECT_EQ(p, nullptr); p = list.find_prev(node2); EXPECT_EQ(p, node1); p = list.find_prev(node3); EXPECT_EQ(p, node2); } |
5.4 删除节点测试
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
// 测试删除节点 TEST(singly_linklist, remove) { int i; singly_linklist<int> list; const list_node<int> *p; list_node<int> *node1, *node2, *node3; node1 = new list_node<int>(1); node2 = new list_node<int>(2); node3 = new list_node<int>(3); list.push_front(node1); list.push_back(node2); list.push_back(node3); // 删除中间节点 list.remove(node2); EXPECT_EQ(node1, list.get_head()); EXPECT_EQ(node3, list.get_tail()); EXPECT_EQ(node1->get_next(), node3); // 删除头节点 list.remove(node1); EXPECT_EQ(node3, list.get_head()); EXPECT_EQ(node3, list.get_tail()); EXPECT_EQ(node3->get_next(), nullptr); // 删除尾节点 list.remove(node3); EXPECT_EQ( list.get_head(), nullptr); EXPECT_EQ( list.get_tail(), nullptr); } |
![[leetcode]138-复制带随机指针的链表](https://www.dyxmq.cn/wp-content/themes/begin/prune.php?src=https://www.dyxmq.cn/wp-content/uploads/2020/02/80613-image60b360f89898fe81.png&w=280&h=210&a=&zc=1)
![【每日打卡】[leetcode]876-链表的中间节点](https://www.dyxmq.cn/wp-content/themes/begin/prune.php?src=https://www.dyxmq.cn/wp-content/uploads/2020/03/64d0d-imagece778ab033c9d90d.png&w=280&h=210&a=&zc=1)
![[leetcode]19-删除链表的倒数第N个节点](https://www.dyxmq.cn/wp-content/themes/begin/prune.php?src=https://www.dyxmq.cn/wp-content/uploads/2020/02/74739-imageb1b50eb343776b42.png&w=280&h=210&a=&zc=1)
![[leetcode]199-二叉树的右视图](https://www.dyxmq.cn/wp-content/themes/begin/prune.php?src=https://www.dyxmq.cn/wp-content/uploads/2020/04/f24a8-image.png&w=280&h=210&a=&zc=1)
![【每日打卡】[leetcode]72-编辑距离](https://www.dyxmq.cn/wp-content/themes/begin/prune.php?src=https://www.dyxmq.cn/wp-content/uploads/2020/04/88c60-imageff84a6c5047db6ed.png&w=280&h=210&a=&zc=1)
![【每日打卡】[leetcode]460-LFU缓存](https://www.dyxmq.cn/wp-content/themes/begin/prune.php?src=https://www.dyxmq.cn/wp-content/uploads/2020/04/5b3f2-image.png&w=280&h=210&a=&zc=1)
![[leetcode]125-验证回文串](https://www.dyxmq.cn/wp-content/themes/begin/prune.php?src=https://www.dyxmq.cn/wp-content/uploads/2020/03/5bfa5-image.png&w=280&h=210&a=&zc=1)
![【每日打卡】[程序员面试宝典]17.16-按摩师](https://www.dyxmq.cn/wp-content/themes/begin/prune.php?src=https://www.dyxmq.cn/wp-content/uploads/2020/03/9ecc9-image.png&w=280&h=210&a=&zc=1)
![【每日打卡】[剑指offer]面试题40-最小的k个数](https://www.dyxmq.cn/wp-content/themes/begin/prune.php?src=https://www.dyxmq.cn/wp-content/uploads/2020/03/c83c9-imagec745c425c670e18c.png&w=280&h=210&a=&zc=1)
![【每日打卡】[leetcode]-409最长回文子串](https://www.dyxmq.cn/wp-content/themes/begin/prune.php?src=https://www.dyxmq.cn/wp-content/uploads/2020/03/e5589-image788d511d7c1e839c.png&w=280&h=210&a=&zc=1)
![【每日打卡】[leetcode]面试题1.6-字符串压缩](https://www.dyxmq.cn/wp-content/themes/begin/prune.php?src=https://www.dyxmq.cn/wp-content/uploads/2020/03/776bc-image.png&w=280&h=210&a=&zc=1)
评论